作者:季凌雲,陆伟,卓辉,李佐健
单位:安徽理工大学 安全科学与工程学院
文章刊发:《煤炭经济研究》2023年第4期
选取秦皇岛港口动力煤价格作为研究对象,搜集10年间煤价数据并分析其影响因素,确定煤炭产量、港口库存、运输成本、火力发电量及社会用电量为主要影响因素;分别建立ARIMA (2,1,2)模型和RF(随机森林)模型并优化,通过加权平均法得到ARIMA和RF模型权重,建立ARIMA-RF组合模型。该模型较深度神经网络模型(DNN)、支持向量回归模型(SVR)、ARIMA模型、RF模型预测的煤价准确度更高,可准确预测动力煤价格走势,为调控能源消费强度、深化能源体制机制改革政策制定提供参考。
关键词:煤价预测;ARIMA模型;随机森林模型;组合模型;精度优化
1.1 数据选取
动力煤在不同的港口往往价格差距甚大, 为了能公平客观地体现市场面上的动力煤价, 各个相关机构一般使用港口平仓价格作为动力煤的价格指标。秦皇岛港处于环渤海经济圈中, 是环渤海十大港口之一, 也是国家唯一直接进行管理的港口; 同时作为煤炭输出港口, 每年的煤炭吞吐量超过2亿t。本文选取秦皇岛港口动力煤价格作为研究对象, 对其近10年动力煤价的形成进行解析。我国煤炭行业在运输方面基本形成 “西煤东送, 北煤南输”的总体格局。煤炭从西部产出后, 通过铁路或公路运输集中到沿海港口, 再通过装船从海上运送到长江三角洲和珠江三角洲,之后通过陆路交通运输到各个火力发电厂。通过对其中的供需关系进行分析,初步提炼出影响煤价的基本指标,见表1。

1.2 数据清洗
数据补插方法有补插均值、中位数、众数,使用固定值,最近邻补插,回归方法和数学插值法。本文使用的数据完整性较好,且通过对比,采用均值插补法最佳。不同指标数据时间频度有较大差异,本文使用EViews软件进行数据转频。将选定的2011—2022年的煤炭产量(月)、火力发电量(月)和社会用电量(月)所有数据以Sum为基准的二次插值,转为2011—2022年的周度数据。将2011—2022年的港口库存(日)和动力煤价格(日)以Average为基准的二次插值,同样转成同频的周度数据。
1.3 相关性分析
首先对完成数据清洗后的数据进行相关性分析,初步了解数据间的线性关系,为后文的分析提供依据。本文使用皮尔森相关系数对数据进行分析,X、Y为需要进行相关性分析的数据对象,xi、yi为这2个对象的取值,见下式。
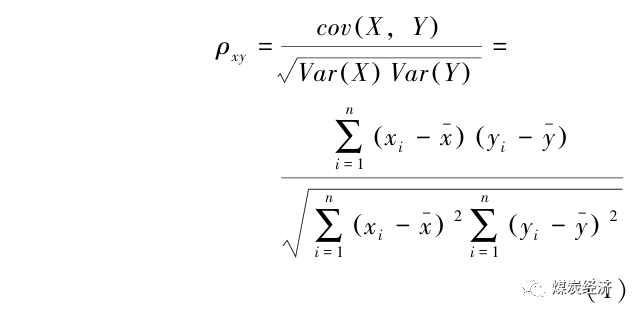
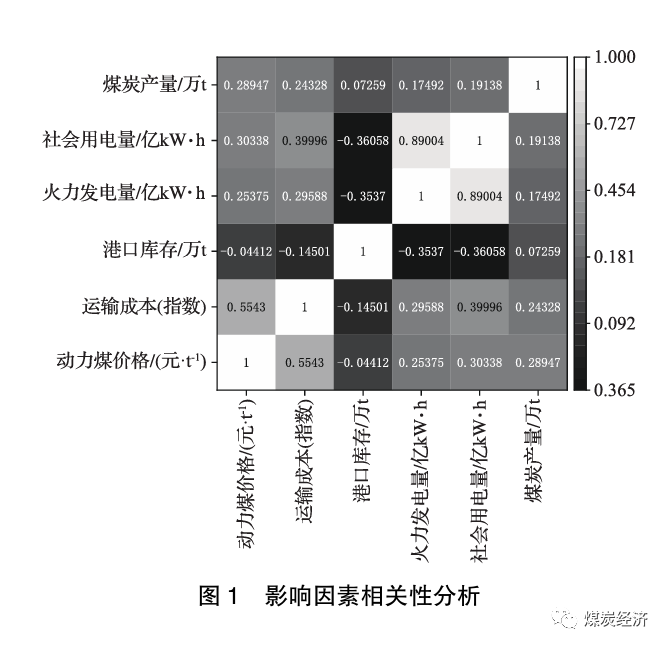
通过Python运算后得出的效果图如图1所示。由图1初步分析可知,动力煤的价格与运输成本、火力发电量、社会用电量和煤炭产量呈现正相关,且与运输成本关联性最大,呈强相关态;动力煤的价格与港口库存呈现负相关。这与初步分析基本一致,验证表明数据选取相对正确,具有可靠性。
1.4 因子分析
因子分析是一种常用的统计分析方法,通常采用SPSS软件进行统计分析。它通过对变量之间的相关系数矩阵进行计算,并依据数据之间的相关性对变量进行分组,使强相关的数据分为一组,弱相关或不相关的数据分到不同组;而后选举出代表每组中数据基本趋势的新变量作为公共因子,将多个指标聚合成两三个公共因子,从而达到降低变量维度的目的。
第1步是检验KMO和Bartlett数值,以此判断因子分析的适用性。KMO值在0.9以上,说明因子分析的适用性极强;在0.7~0.9之间表示强; 0.6~0.7之间适中;0.5~0.6之间表示弱;0.5以下极弱。将动力煤价格及煤价影响因素数据导入SPSS软件中进行检验,结果见表2。

可以看出,KMO统计量为0.605,在程度上,本数据进行后续分析具有合理性。Bartlett球度检验的显著性为1%,水平上呈现显著性,拒绝原假设,各变量间具有相关性,因子分析有效。
通过分析总方差解释表和旋转后因子载荷系数表,查看因子数和对数据解释效果。总方差解释表主要是看因子对于变量解释程度的贡献率,若贡献率太低,说明总体解释效果差,则需要调整因子数量;旋转后因子载荷系数表的作用是查看每个因子对所有输入数据的解释效果,数值越高表示本因子对当前变量解释效果越好;共同度是所有因子对当前变量的综合解释度,数值与解释效果呈现正相关。利用SPSS软件分析得总方差解释表和旋转因子载荷系数,见表3和表4。
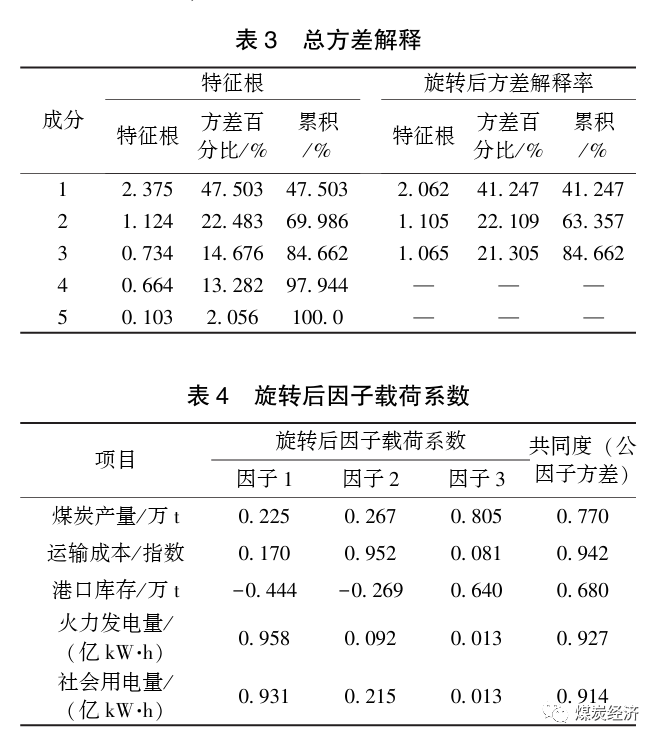
在方差解释表中,当主成分为3时,总方差解释的特征根低于1.0,总方差解释率达到84.662%,对原始数据有着较为不错的总体解释效果。旋转后因子载荷系数表中,3个因子分别对5组原始数据的公因子方差最低为0.680,处于0.600标准以上,对所有单个数据都有着较好的解释水平。验证表明公共因子的选择较为成功。
最后通过分析成分矩阵,利用提取到的3个公共因子对原始数据进行定义。成分矩阵见表5。
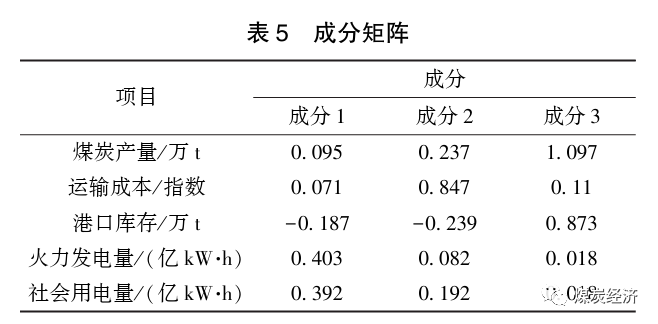
利用上表计算出成分得分,得出主成分公式如下。

2.1 ARIMA模型
ARIMA模型即自回归积分滑动平均模型,是一种通过历史时间序列数据预测未来一段时间目标数据的预测方法,由自回归滑动平均(ARMA)模型扩展而来。时间序列模型主要包括AR(p)模型(自回归),p为自回归移动阶数;MA(q)模型(滑动平均),q为移动平均阶数;ARMA(p,q)模型(回归滑动平均);ARIMA(p,d,q)模型(自回归积分滑动平均),d为差分阶数。
AR(p)模型,如果时间序列{Xt }满足下式,则说明其是自回归移动阶数为p阶的自回归模型。
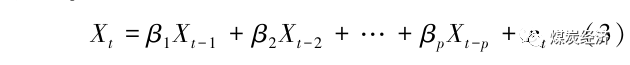
其中,Xt为待预测的期望值,Xt-o为之前o期的值,对应的βo为该数值的系数;εt为1个独立同分布的随机变量序列,其均值为零,方差大于零,即纯随机序列,又称为白噪声序列。
MA(q)模型,如果序列{Xt }满足下式,说明其是移动平均阶数为q阶的滑动平均模型。
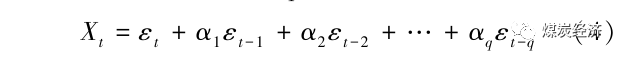
其中,Xt意义同上;εt-o为过去o期对应的随机干扰值,对应αo为此数据的系数。ARMA(p,q)模型,此自回归滑动平均过程中的序列{Xt },满足下式。
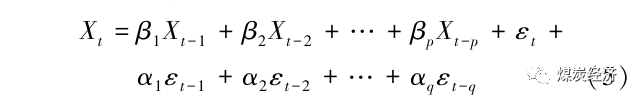
其中,Xt、Xt-i、βi、εt-i、αi和AR(p)、MA (q)模型中的含义相同。
以上3个时间序列模型都是基于平稳的时间序列。当时间序列因为具有趋势性而不平稳后,需要对其进行必要的d次差分,以消除趋势影响,使之平稳;然后可使用ARMA(p,q)模型,进行分析预测。
ARIMA(p,d,q)模型,自回归积分滑动平均过程的非平稳序列{Yt }满足下式。
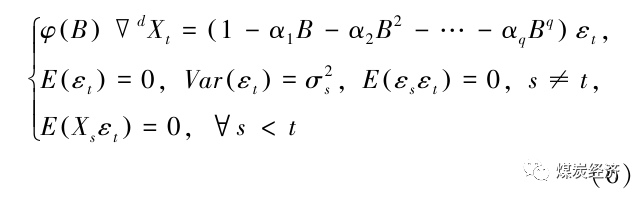
其中,∇d=(1-B)2,B是后移算子,∇为差分符号,σs是纯随机序列εt的方差,其他符号含义与AR(p)、MA(q)、ARMA(p,q)模型的含义相同。
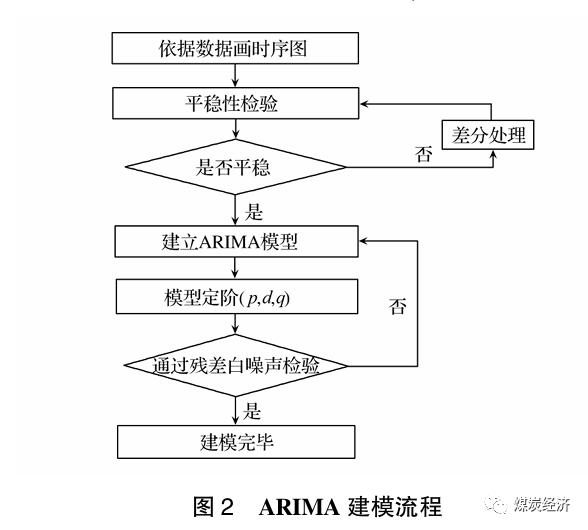
ARIMA模型的算法实现过程,如图2所示。
2.2 RF模型
随机森林(RF)算法是为了解决单一决策树模型存在的缺陷,将多个决策树模型进行叠加,形成“森林”,以此预测最终的结果。它的输出是若干决策树输出的集合。决策树算法是一种经典的机器学习算法,其本质是数据结构中的二叉树,开始只有根节点,通过不断划分生成新的节点,连接节点之间的线为有向边,叶节点是决策树中最顶端的节点,决策树唯一的输出是从根节点到某个叶节点的路径的值。决策树需要使用预处理过的数据作为训练样本进行构建。节点划分的依据是节点的“纯度”,即划分后的节点“纯度”要高于划分前,否则将不对此叶节点进行划分。一般采取 “基尼值” (Gini)来表示节点样本数据间的纯度,计算过程如下。
1)样本 Gini 指标计算。
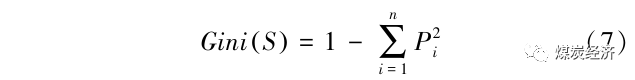
其中,S为数据集合,n为样本类别数目,Pi为S中第i类样本所占的比例。Gini(S)表示从数据集S中随机选择2个样本的类别标记不同的概率。Gini(S)越小,则数据集S的纯度越高。
2)样本集S被划分为2个子集S1与S2 ,此次划分的Gini 指标见下式。在节点分裂时,每个划分的Gini指标Ginisplit (S)越小,表示划分越合理,数据集的纯度越高。
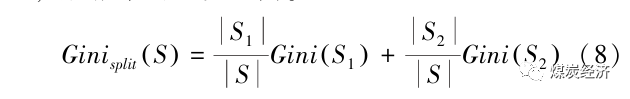
单棵决策树模型能够处理多种数据类型,且能够较好抑制噪声与处理缺失值,但是较为复杂的分类规则也使决策树模型易陷入过拟合的状态。所以在其之上改进,引入随机森林的思想。首先在原始训练数据样本集S中随机抽取k个单独样本进行训练,下次抽取之前,都将之前的样本放回到原始训练集S中。每次抽取的k个单独样本都将生成1个决策树,每棵决策树都具有相同的分布类型,统计所有决策树,按特定方法输出森林的结果。最简单且常用的方法为线性集成:当输入数据时,对所有决策树的结果投票,每棵决策树占1票,哪种类型被投票最多,即为样本最终的输出结果。网格搜索法可以通过对RF模型中的各个参数进行穷举遍历,最终获取的超参数组合最优,来实现RF模型的优化。
虽然Grid search遍历所有的组合,具有耗时较久的缺点,但和手动调参相比,它既具备优秀的速度,又能使误差最小,所以本文采用Grid search穷举遍历来优化RF模型。
2.3 ARIMA-RF模型
组合模型通常有2种方法:串联法和并联法。一般都进行时间序列预测的模型,采用串联法组合模型。串联法先用甲模型得到预测残差值Re,再通过残差值Re建立乙模型,得到残差修正值,最后两者取合得预测结果。并联法则需要确定各组合模型的权重值,确定权重的常见方法有等权重法、简单加权平均法(式(9))、预测误差平方和倒数法(式(10))和误差方差均方倒数法(式(11))。
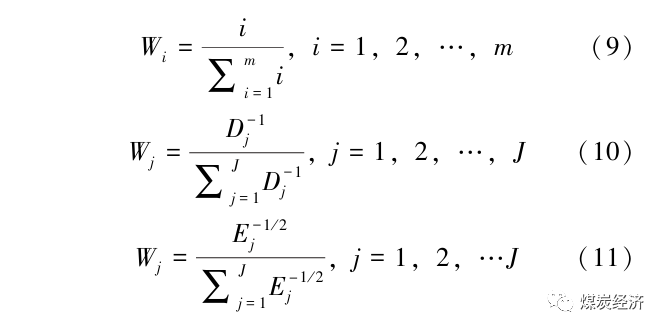
式 (10) 中, Dj 为第J个模型的误差平方和;式 (11) 中, Ej 为第J个模型的预测误差方差。
本文使用并联组合法中的简单加权法建立ARIMA-RF 组合模型, 该组合模型流程如图3所示。
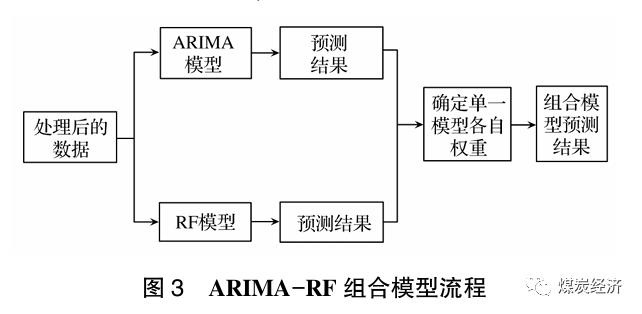
3 实例验证
3.1 ARIMA实证分析
利用2011 年12月9日至2022年4月1日的秦皇岛动力煤 (Q5500) 价格的周度数据建立时间序列图。图4为2011年12月9日至2022年4月1日的动力煤价格X的趋势图。由图可知, 煤价序列无明显季节性波动, 但无持续的增长或减少的趋势,应对数据进行平稳性分析。
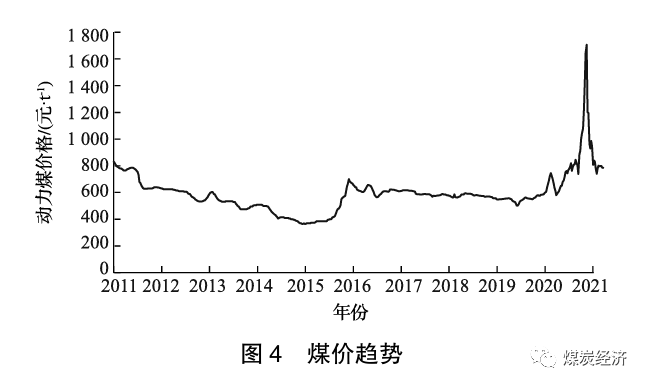
通过单位根检验中的ADF方法验证序列是否具有平稳性。ADF检验的结果为-2.25, 5%的临界值为-2.87, 结果明显大于5%的值, 显然不能显著地拒绝原假设, 原假设为序列是非平稳序列; P值为0.19, 且不十分接近于零。基于以上两者, 可以认为原始序列是非平稳序列。
对原始非平稳序列X进行一阶差分, X′是差分后的序列, 图5为序列X′的趋势图, 发现差分序列各值围绕均值上下波动, 其ADF 检验结果为-6. 29, 小于1%的临界值-3.44, 且 P 值为3.67× 10-8, 小于显著性水平(0.05), 所以拒绝原假设。原假设为序列是不平稳序列, 即一阶差分后序列平稳, 因此该ARIMA (p, d, q) 模型的d取1。
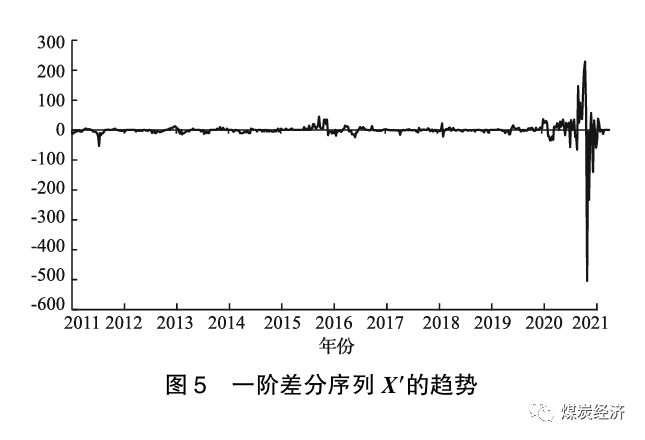
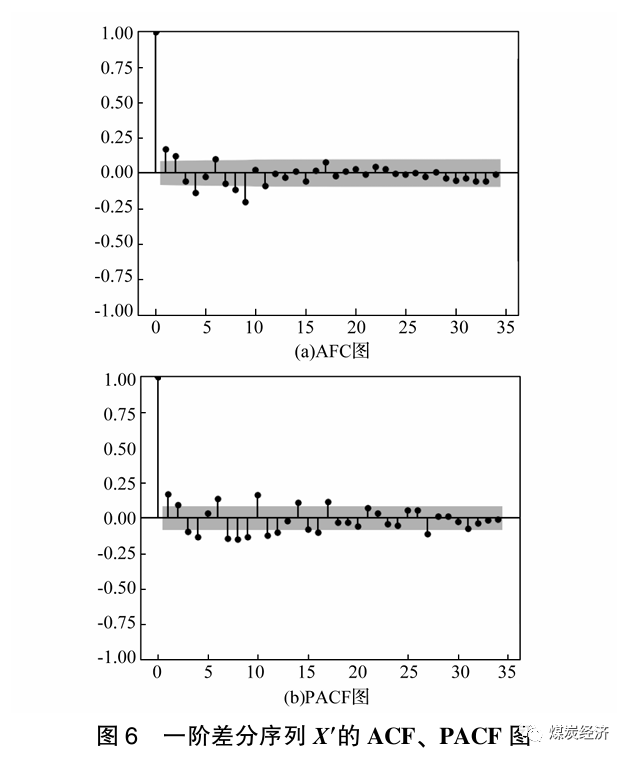
图6为序列X′的自相关系数 (ACF) 和偏自相关系数 (PACF) 图。由图可知, ACF和PACF图的截尾、拖尾都不显著。观察落于置信边界外的阶数, 根据PACF 图, 可得 p 可选0、1、2、3、4、6、8、9、 10; 根据ACF图, 可得q可选0、1、2、4、6、8、9。为给模型定阶, 根据BIC (贝叶斯信息) 准则, 通过网格搜索法, 确定BIC最优的参数p、q。BIC 准则公式如下。
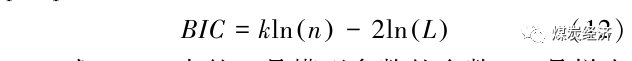
式 (12) 中的k是模型参数的个数, n是样本数量, L是似然函数。贝叶斯准则的结果越小越好, BIC 结果在p=2且q=2时最小, 由此确定p=2, q= 2, p、q 的结果也在ACF和PACF图显示的范围中。所以得到2011年12月9日至2022年4月1日的动力煤价格时间序列模型ARIMA (2,1,2)。
对2011 年12月9日至2022年4月1日的动力煤价格的残差序列Xr 绘制ACF图和PACF图, 如图7所示。图8则为残差序列Xr的QQ图。由图可知,序列Xr有短期相关性,相关系数趋向于零,残差是纯随机序列。
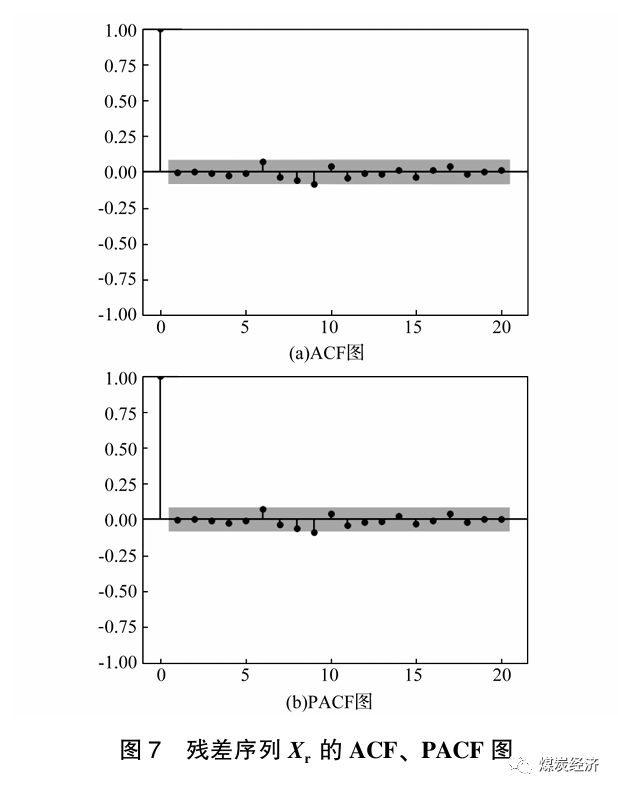

对残差序列Xr进行LB检验(Ljung-Box test), P值为0.91,不小于显著性水平(0.05),所以接受原假设:相关系数为零,即相关系数和0没有显著性差异,残差序列Xr为纯随机序列。
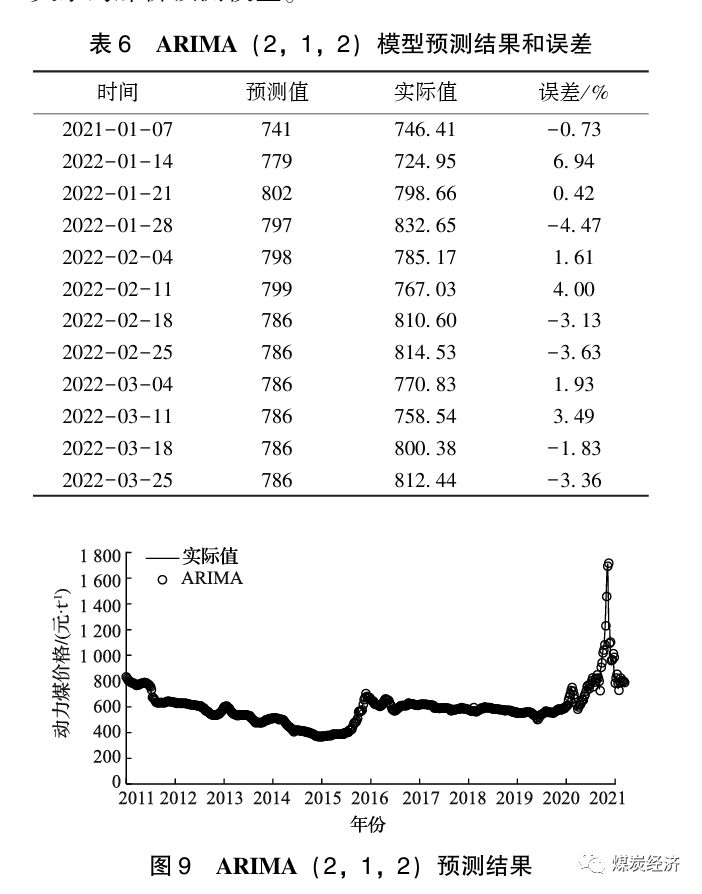
用ARIMA(2,1,2)模型预测2022年1月7日至2022年3月25日的秦皇岛动力煤(Q5500)价格,结果见表6。煤炭价格的预测值与实际值的平均误差为2.48%,是较为理想的结果。
2011年12月9日至2022年4月1日的秦皇岛动力煤(Q5500)价格的ARIMA(2,1,2)预测值与实际值的对比如图9所示。由图可知,10年间秦皇岛动力煤(Q5500)价格在ARIMA(2,1,2)模型下的预测值和实际值的趋势大体一致,但模型平均的均方误差(MSE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)分别为939.05、30.64和0.91,结果不是很理想。综上,本文将引入RF算法,以寻求精度更高、兼顾线性和非线性关系的煤价预测模型。
3.2 ARIMA-RF实证分析
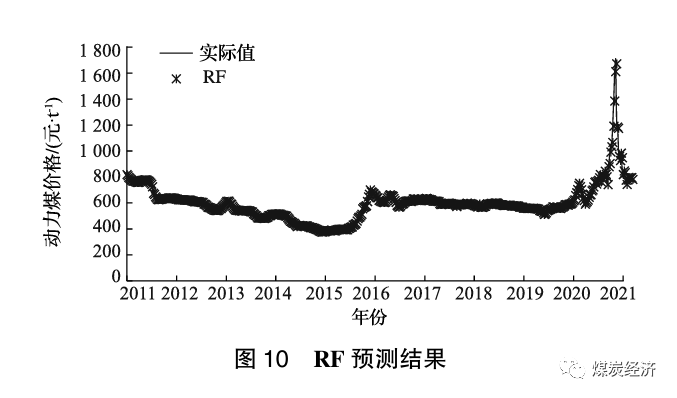
采用公因子数据作为RF模型的输入,2011年12月9日至2022年2月25日的动力煤价格为输出。遵循训练集与测试集之比为3∶1的原则,将2011年至2019年的动力煤价格作为训练集,2020年至2021年的动力煤价格作为测试集。对建立的RF模型采用网格搜索法进行超参数优化,并检验泛化性能。RF模型的MSE、RMSE和MAPE的值分别为934.44、30.57和0.52。预测出下一周(2022年3月4日)的煤价为785.37,与真实值786相比,误差为-0.08%。使用RF模型预测2021年4月2日至2022年2月25日的动力煤价格,结果如图10所示。
基于以上优化后的ARIMA(2,1,2)和RF模型,通过并联组合方法对两者的预测结果进行加权组合,得到组合后的2011年12月9日至2022年2月25日的动力煤价格预测结果。由于2个子模型预测的误差方差已知, 不宜采用等权平均组合方法,故采用简单加权平均法更适宜。在简单加权平均法中, 误差方差和权重系数成反比, 误差小的预测值应具有更大的赋权比例, 误差大的预测值将得到更小的赋权比例。本文通过Python, 以MAPE最小为目标, 从0~1遍历, 分别得到ARIMA模型的权重为0.88, RF模型的权重为0.12。ARIMA-RF 模型的MSE、RMSE 和 MAPE 分别为 924.94、30.41 和0.17。采用ARIMA-RF 模型预测2021年4月2日至2022年2月25日的动力煤价格, 结果如图11所示。
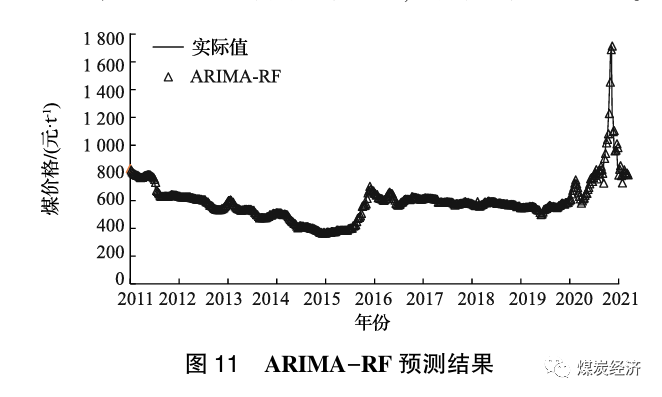
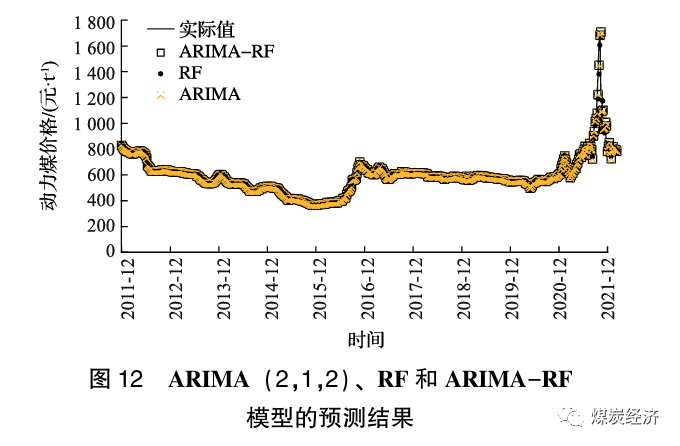
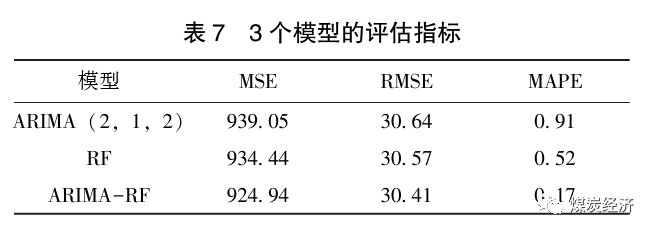
ARIMA-RF 模型预测的下一周(2022年3月4日) 的煤价为785.63。ARIMA (2, 1, 2)、RF和ARIMA-RF模型的预测结果如图12 所示, 3个型的评估指标见表7。由图12可知, 3个模型2012年到2022年的拟合曲线与实际结果近似; 由表7可知, 组合模型的MSE、RMSE、MAPE 值在3种模型中均为最小, 因此该ARIMA-RF的组合模型用于动力煤价格的预测切实可行。
3.3 抽样对比分析
为验证本文组合模型具有更好的准确度, 选择深度神经网络 (DNN) 模型、支持向量回归(SVR) 模型、ARIMA模型和RF模型作为参照模型, 与ARIMA-RF 模型作对比分析。DNN神经网络模型和SVR模型作为已用于煤价预测的成熟机器学习模型, 选择其作为对比组分析具有代表性; ARIMA 模型和RF模型作为参照组, 描述了组合模型的适用性。由于2021年政策影响, 限电停电导致2021 下半年煤价变化幅度过大, 所以选取2021年第三季度进行预测分析, 同时分别抽选2019年、2020 年第1、3季度和2021年第1季度进行动力煤价格的滚动预测对比分析, 如图13所示。
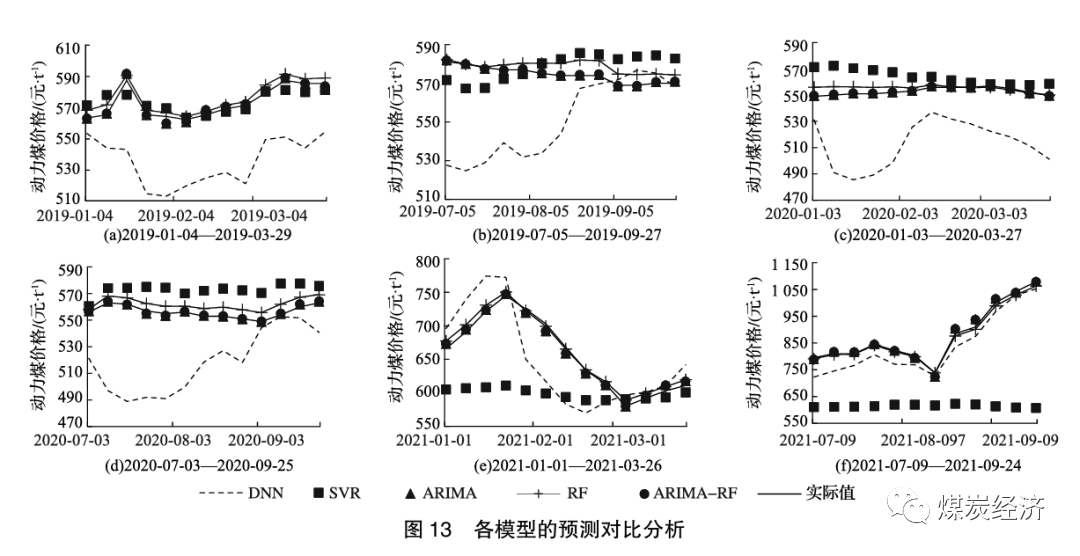
表8为5种模型2019年、2020年和2021年第1、3 季度的RMSE。
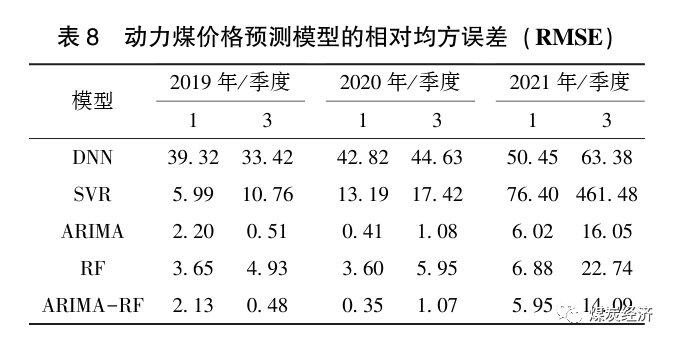
由图13和表8可知, ARIMA-RF模型的准确性明显高于对照组的4种模型。通过图13 (a) 与另外5个图的对比, 可以看出在煤价较为平稳时, SVR 模型的预测效果优于DNN模型; 而当煤价波动幅度较大时, SVR模型的预测效果远低于DNN模型。ARIMA模型和RF模型这2种模型的预测效果明显比DNN 模型和SVR 模型的预测效果更优秀, 源于已经对前2种模型进行超参数优化, 寻优后的ARIMA模型和RF模型拥有更高的准确性。基于ARIMA模型和RF 模型组合而成的ARIMA-RF模型经过加权组合, 在前两者基础上进一步降低了误差, 在5种模型中具有最高的准确度。
针对国内动力煤价格非线性、受政策影响大和供需关系存在滞后性的问题,本文提出了一种基于ARIMA-RF的煤价预测组合模型,较经典的DNN模型、SVR模型、ARIMA模型和RF模型准确度更高,可为政府调控能源消费强度、深化能源体制机制改革、确保能源安全稳定供应和平稳过渡提供参考。通过本文研究,可以得到如下结论。
1)通过均值插补法和二次插值法进行数据清洗与转换,实现数据的预处理;根据皮尔森相关系数和类似主成分的因子分析,为动力煤价格的影响因素提供可靠性。
2)建立ARIMA(2,1,2)模型和RF模型并优化,在此基础上,通过加权平均法得到子模型权重,建立ARIMA-RF组合模型。将其与子模型及经典DNN和SVR模型对比,验证出ARIMA-RF模型具有更好的回归预测结果及更高的准确度与精确度。
3)本文提出的ARIMA-RF模型可准确预测下一周煤价,缓解了滞后性对煤价的影响,可为企业合理预估煤价降低成本及政府制定政策提供一定参考,确保煤炭稳定供应,保障煤炭生产、流通、消费等环节平稳运行,有助于我国深化能源体制机制改革,早日实现“双碳”目标。
整理发布:张雅惠(实习)
审核:李修东
电话:010-84261852
邮箱:mtjjyj2015@126.com
网站:www.mtjjyj.com
声明:《煤炭经济研究》已刊发此文,享有本论文数字化复制权、发行权、汇编权及信息网络传播权。转载或者引用本文内容请注明来源,对于不遵守此声明或者其他违法使用本文内容者,《煤炭经济研究》依法保留追究权。







